La regresión.
En varias entradas de Series de Tiempo y de Machine Learning en R comenté sobre la regresión lineal. El método es bien conocido en varios campos y quizás es el más natural de aprender, ya que la idea de trazar la recta que mejor describe la relación entre puntos de un plano parece familiar e intuitivo.
El problema con el método o el modo en que se enseña pude variar, como el método en ocasiones se subvalora debido a que ese considera en general que es solo «agregar línea de tendencia» a los datos, pero se deja de lado la revisión de los estadísticos y de revisar el comportamiento de los errores de la estimación.
En la entrada de manera breve comento un pequeño recorrido sobre las técnicas de regresión clásica y las penalizadas. Las principales referencias sobre las cuales comento los métodos son [1,2] y algunos artículos o reportes que dejo en las referencias. Lo que ya no comento es la parte estadística; es decir, los detalles sobre las pruebas de hipótesis y las potencias de las pruebas las comenté en otras entradas. En esta trato de solo mencionar lo mínimo sobre esos detalles, pero enfocarme más en otros usos y las variaciones a la técnica tradicional.
El modelo en general.
La idea de la regresión es tener un conjunto de datos de entrada y explicar o describir las salidas como una combinación lineal de los datos de entrada.
Es decir, se tienen los datos: 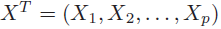
y el modelo que se pretende describir es:
En la ecuación anterior se interpreta como la salida del modelo f(X) sea lo más parecida a Y, que son los valores reales a estimar.
Para el caso de los mínimos cuadrados se tiene que la función a minimizar es:
Lo que se hace es sustituir la expresión que de f(x) que depende de las β’s para minimizar la ecuación, lo que se hace es tratar de encontrar los mejores β’s para describir Y.
En los métodos modernos lo que se penalizar la estimación de los β’s, debido a que al estimar la regresión por mínimos cuadrados sobre un subconjunto de entrenamiento ( train set) de los datos, es decir algunos de los x’s, permite obtener los parámetros β’s sobre estimados y al momento de usar el modelo para el conjunto de datos de prueba (test set) se obtienen tasas de errores mayores.
Los métodos con penalización usuales son Ridge y Lasso, los dos agregan un parámetro λ que implica el problema de tener un método para definir el mejor valor para el modelo. Explico con ejemplos que se hace para determinar el parámetro.
Para el modelo Ridge a la función de errores es como la de los mínimos cuadrados pero agregando un término más. La ecuación es la siguiente:
Para el modelo Lasso es similar a la de Ridge, pero en la penalización en lugar de considerar los β’s al cuadrado se considera su valor absoluto. La ecuación es la siguiente:
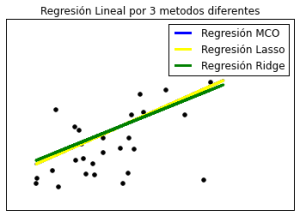
Lamento poner las ecuaciones, pero creo que pese a que no se entienda la teoría de manera total , al observando las diferencias en las ecuaciones se puede apreciar la diferencia en los métodos. En la primera gráfica de la entrada no lo mencioné, pero si se presiona sobre la imagen y se observa con cuidado que tiene trazadas 3 rectas sobre los datos de color negro, estas tres rectas corresponden a los 3 métodos distintos.
Una visión o idea gráfica de lo que pasa con el modelo o técnica, es visto en la siguiente imagen. Al final el objetivo de la regresión lineal es encontrar el plano que mejor satisface ciertas condiciones para asegurar que predice o explica lo mejor posible los datos.
Ejemplo 1
Para visualizar la diferencia en las estimaciones haciendo uso de Python, sobre todo de la librería scikit-learn hago uso del código de Jaques Grobler, modifico parte de su código para agregar la estimación de la regresión Rigde y Lasso, además elijo una muestra mayor de datos para prueba para que la gráfica sea notoriamente más atractiva.
Lo que hace el código:
- Se toma una base de datos sobre diabetes la cual se puede cargar directamente en la librería scikit-learn.
- Se divide la muestra en datos de entrenamiento( train) y de prueba (test).
- Se estiman los 3 modelos de regresión y se estiman los estadísticos base de las estimaciones.
- Se hace la gráfica de los datos de test.
# -*- coding: 850 -*-
print(__doc__)
# Code source: Jaques Grobler
# License: BSD 3 clause
#Se cargan los modulos
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
# Se cargan los datos
diabetes = datasets.load_diabetes()
# Se usa cierta muestra de los datos
diabetes_X = diabetes.data[:, np.newaxis]
diabetes_X_temp = diabetes_X[:, :, 2]
# Se separa la muestra de datos
diabetes_X_train = diabetes_X_temp[:-30]
diabetes_X_test = diabetes_X_temp[-30:]
# Se separa las variables explicadas
diabetes_y_train = diabetes.target[:-30]
diabetes_y_test = diabetes.target[-30:]
# Se crean los modelos lineales
regr = linear_model.LinearRegression()
regr2=linear_model.Lasso(alpha=.5)
regr3=linear_model.Ridge(alpha=.5)
#Se entrenan los modelos
regr.fit(diabetes_X_train, diabetes_y_train)
regr2.fit(diabetes_X_train, diabetes_y_train)
regr3.fit(diabetes_X_train, diabetes_y_train)
print u'Regresión Mínimos Cuadrados Ordinarios'
# Coeficiente
print'Coeficientes:',regr.coef_
# MSE
print("Residual sum of squares: %.2f"
% np.mean((regr.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# Varianza explicada
print('Varianza explicada: %.2f\n' % regr.score(diabetes_X_test, diabetes_y_test))
print u'Regresión Lasso'
# Coeficiente
print'Coeficientes:', regr2.coef_
# MSE
print("Residual sum of squares: %.2f"
% np.mean((regr2.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# Varianza explicada
print('Varianza explicada: %.2f\n' % regr2.score(diabetes_X_test, diabetes_y_test))
print u'Regresión Ridge'
#Coeficiente
print'Coeficientes:', regr3.coef_
# MSE
print("Residual sum of squares: %.2f"
% np.mean((regr3.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# Varianza explicada
print('Varianza explicada: %.2f\n' % regr3.score(diabetes_X_test, diabetes_y_test))
# Plot
plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, regr.predict(diabetes_X_test), color='blue',
linewidth=3, label=u'Regresión MCO')
plt.plot(diabetes_X_test, regr2.predict(diabetes_X_test), color='yellow',
linewidth=3, label=u'Regresión Lasso')
plt.plot(diabetes_X_test, regr3.predict(diabetes_X_test), color='green',
linewidth=3, label=u'Regresión Ridge')
plt.title(u'Regresión Lineal por 3 metodos diferentes')
plt.legend()
plt.xticks(())
plt.yticks(())
plt.show()
Los resultados serían los siguientes:
Regresión Mínimos Cuadrados Ordinarios Coeficientes: [ 941.43097333] Residual sum of squares: 3035.06 Varianza explicada: 0.41 Regresión Lasso Coeficientes: [ 720.32135439] Residual sum of squares: 3265.36 Varianza explicada: 0.37 Regresión Ridge Coeficientes: [ 612.64202818] Residual sum of squares: 3458.17 Varianza explicada: 0.33
La gráfica se vería de la siguiente forma:
El ejemplo anterior viendo la gráfica y los estadísticos tenemos como conclusión que le método MCO; mínimo cuadrados ordinarios, es el que mejor se ajusta a nuestros datos. En este caso uno se pregunta sobre la ventaja de usar otro método para la regresión lineal, si los resultados son favorables para la técnica más conocida.
Lo que no se menciona en el código, o lo que se queda sin explicar es la elección de λ para los modelos Ridge y Lasso. Lo que se hace para aplicar un buen modelo de estos dos métodos, es estrenar el modelo de modo tal que el valor de λ sea el «mejor». Para esto se usa Cross-Validation, así que haciendo ligeros cambios al código anterior se puede mejorar la aplicación de los modelos lineales.
# -*- coding: 850 -*-
print(__doc__)
# Code source: Jaques Grobler
# License: BSD 3 clause
#Se cargan los módulos
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
# Se cargan los datos
diabetes = datasets.load_diabetes()
# Se eligen las muestras de datos
diabetes_X = diabetes.data[:, np.newaxis]
diabetes_X_temp = diabetes_X[:, :, 2]
# Se dividen los datos en training/testing
diabetes_X_train = diabetes_X_temp[:-30]
diabetes_X_test = diabetes_X_temp[-30:]
# Se divide la variable explicada en training/testing
diabetes_y_train = diabetes.target[:-30]
diabetes_y_test = diabetes.target[-30:]
# Se crean los modelos lineales
regr = linear_model.LinearRegression()
#regr2=linear_model.LassoCV(alpha=)
regr3=linear_model.RidgeCV(alphas=[0.1,0.2,0.5,1.0,3.0,5.0,10.0])
# Se entrenan los modelos
regr.fit(diabetes_X_train, diabetes_y_train)
regr2=linear_model.LassoCV(cv=20).fit(diabetes_X_train, diabetes_y_train)
regr3.fit(diabetes_X_train, diabetes_y_train)
print u'Regresión Mínimos Cuadrados Ordinarios'
# Coeficiente
print'Coeficientes:',regr.coef_
# MSE
print("Residual sum of squares: %.2f"
% np.mean((regr.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# Varianza Explicada
print('Varianza explicada: %.2f\n' % regr.score(diabetes_X_test, diabetes_y_test))
print u'Regresión Lasso'
# Coeficientes
print'Coeficientes:', regr2.coef_
# MSE
print("Residual sum of squares: %.2f"
% np.mean((regr2.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# Varianza Explicada
print('Varianza explicada: %.2f\n' % regr2.score(diabetes_X_test, diabetes_y_test))
print u'Regresión Ridge'
# Coeficiente
print'Coeficientes:', regr3.coef_
# MSE
print("Residual sum of squares: %.2f"
% np.mean((regr3.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# Varianza Explicada
print('Varianza explicada: %.2f\n' % regr3.score(diabetes_X_test, diabetes_y_test))
# Plot
plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, regr.predict(diabetes_X_test), color='blue',
linewidth=3, label=u'Regresión MCO')
plt.plot(diabetes_X_test, regr2.predict(diabetes_X_test), color='yellow',
linewidth=3, label=u'Regresión Lasso')
plt.plot(diabetes_X_test, regr3.predict(diabetes_X_test), color='green',
linewidth=3, label=u'Regresión Ridge')
plt.title(u'Regresión Lineal por 3 metodos diferentes')
plt.legend()
plt.xticks(())
plt.yticks(())
plt.show()
Lo que se tienen como resultado es lo siguiente:
Regresión Mínimos Cuadrados Ordinarios Coeficientes: [ 941.43097333] Residual sum of squares: 3035.06 Varianza explicada: 0.41 Regresión Lasso Coeficientes: [ 940.48954236] Residual sum of squares: 3035.57 Varianza explicada: 0.41 Regresión Ridge Coeficientes: [ 850.17738251] Residual sum of squares: 3103.11 Varianza explicada: 0.40
La gráfica correspondiente es:
Lo que se aprecia es que los modelos mejoran considerablemente, si bien el modelo MCO sigue siendo uno de los mejores para este ejemplo, algo a considerar es que es una muestra pequeña y de pocas dimensiones. Así que lo interesante es aplicar la regresión a muestras mayores y de datos con una mayor cantidad de variables.
Ejemplo 2-Regresión Multiple
Para el siguiente ejemplo hago uso de una matriz de datos de tamaño 506 líneas de datos con 12 variables de entrada y una variable que se trata de estimar por métodos lineales. Los datos corresponden a los valores de las viviendas en los suburbios de Boston.
Tomo estos datos para mostrar como aplicar la regresión a datos con varia variables, para este caso no hago una gráfica pero se pueden revisar los datos o valores de los estadísticos para tener un modo de elegir entre modelos.
El código es muy similar al anterior y lo que se puede hacer como variación es aplicar alguna técnica de reducción de dimensiones para elegir las variables que «impactan realmente» en el modelo o jugar con ejecutar la regresión no con todas las variables, sino empezar con unas y poco a poco agregar nuevas para revisar como se comporta el modelo al estimar con solo unas cuantas variables. Algo que tampoco hago en este caso es explorar las variables antes de aplicar la regresión, pero la intención es ver que prácticamente es igual la ejecución de una regresión multi lineal.
#import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
#13 variables explicativas
# Se cargan los datos
Boston = datasets.load_boston()
# Se divide en training/testing sets
Boston_train = Boston.data[:405,]
Boston_test = Boston.data[405:,]
# La variable explicativa se divide en training/testing sets
Boston_y_train = Boston.target[:405]
Boston_y_test = Boston.target[405:]
regr = linear_model.LinearRegression()
regr2=linear_model.LassoCV(cv=20).fit(Boston_train, Boston_y_train)
regr3=linear_model.RidgeCV(alphas=[0.1,0.2,0.5,0.7,1.0,1.5,3.0,5.0,7.0,10.0])
#np.size(Boston_y_train = Boston.target[:405])
regr.fit(Boston_train, Boston_y_train)
regr3.fit(Boston_train,Boston_y_train)
print u'Regresión Mínimos Cuadrados Ordinarios'
#Coeficiente
print'Coeficientes:',regr.coef_
# MSE
print("Residual sum of squares: %.2f"
% np.mean((regr.predict(Boston_test) - Boston_y_test) ** 2))
# Varianza explicada
print('Varianza explicada: %.2f\n' % regr.score(Boston_train, Boston_y_train))
print u'Regresión Ridge'
# Coeficientes
print'Coeficientes:', regr3.coef_
# MSE
print("Residual sum of squares: %.2f"
% np.mean((regr3.predict(Boston_test) - Boston_y_test) ** 2))
# Varianza Explicada
print('Varianza explicada: %.2f\n' % regr3.score(Boston_train, Boston_y_train))
print u'Regresión Lasso'
# Coeficiente
print'Coeficientes:', regr2.coef_
# MSE
print("Residual sum of squares: %.2f"
% np.mean((regr2.predict(Boston_test) - Boston_y_test) ** 2))
# Varianza Explicada
print('Varianza explicada: %.2f\n' % regr2.score(Boston_train, Boston_y_train))
Los resultados del código son los siguientes resultados:
Regresión Mínimos Cuadrados Ordinarios Coeficientes: [ -1.94651664e-01 4.40677436e-02 5.21447706e-02 1.88823450e+00 -1.49475195e+01 4.76119492e+00 2.62339333e-03 -1.30091291e+00 4.60230476e-01 -1.55731325e-02 -8.11248033e-01 -2.18154708e-03 -5.31513940e-01] Residual sum of squares: 33.58 Varianza explicada: 0.74 Regresión Ridge Coeficientes: [ -1.93961816e-01 4.42902027e-02 4.66864588e-02 1.87777854e+00 -1.37158180e+01 4.76760163e+00 1.65803755e-03 -1.28477100e+00 4.57255634e-01 -1.57415769e-02 -7.97849246e-01 -1.78511420e-03 -5.33113498e-01] Residual sum of squares: 33.15 Varianza explicada: 0.74 Regresión Lasso Coeficientes: [-0.13537099 0.04758408 -0. 0. -0. 3.26851037 0.01014632 -0.9131925 0.39587576 -0.01796467 -0.65864709 0.00511243 -0.67828222] Residual sum of squares: 23.48 Varianza explicada: 0.71
Si se tienen cuidado se puede observar que los dos primeros modelos muestran mucha «cercanía», los dos tienen estimaciones casi similares y estadísticos muy parecidos. El modelo Lasso al contrario, parece considerablemente diferente y con valores considerablemente diferentes. El punto clave es cómo elegir entre los modelos. En esta parte sería adecuado hacer uso de algunos indicadores sobre la calidad del modelo como AIC o BIC, etc.
Ejemplo 3. Usando la regresión de otro modo.
El siguiente ejemplo es un ejemplo que considero bastante bonito y muestra el uso de Lasso y Ridge que en general no se piensa, respecto el código y el reconocimiento a Emmanuelle Gouillart, sobre la cual recomiendo revisar su tutorial sobre procesamiento de imágenes. No hago cambio alguno al código, lo que hago es explicar que hace en cada etapa para clarificar y valorar las regresiones con penalización como herramientas de reconstrucción de imágenes.
El código:
print(__doc__)
# Author: Emmanuelle Gouillart <emmanuelle.gouillart@nsup.org>
# License: BSD 3 clause
import numpy as np
from scipy import sparse
from scipy import ndimage
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
import matplotlib.pyplot as plt
def _weights(x, dx=1, orig=0):
x = np.ravel(x)
floor_x = np.floor((x - orig) / dx)
alpha = (x - orig - floor_x * dx) / dx
return np.hstack((floor_x, floor_x + 1)), np.hstack((1 - alpha, alpha))
def _generate_center_coordinates(l_x):
l_x = float(l_x)
X, Y = np.mgrid[:l_x, :l_x]
center = l_x / 2.
X += 0.5 - center
Y += 0.5 - center
return X, Y
def build_projection_operator(l_x, n_dir):
""" Compute the tomography design matrix.
Parameters
----------
l_x : int
linear size of image array
n_dir : int
number of angles at which projections are acquired.
Returns
-------
p : sparse matrix of shape (n_dir l_x, l_x**2)
"""
X, Y = _generate_center_coordinates(l_x)
angles = np.linspace(0, np.pi, n_dir, endpoint=False)
data_inds, weights, camera_inds = [], [], []
data_unravel_indices = np.arange(l_x ** 2)
data_unravel_indices = np.hstack((data_unravel_indices,
data_unravel_indices))
for i, angle in enumerate(angles):
Xrot = np.cos(angle) * X - np.sin(angle) * Y
inds, w = _weights(Xrot, dx=1, orig=X.min())
mask = np.logical_and(inds >= 0, inds < l_x)
weights += list(w[mask])
camera_inds += list(inds[mask] + i * l_x)
data_inds += list(data_unravel_indices[mask])
proj_operator = sparse.coo_matrix((weights, (camera_inds, data_inds)))
return proj_operator
def generate_synthetic_data():
""" Synthetic binary data """
rs = np.random.RandomState(0)
n_pts = 36.
x, y = np.ogrid[0:l, 0:l]
mask_outer = (x - l / 2) ** 2 + (y - l / 2) ** 2 < (l / 2) ** 2
mask = np.zeros((l, l))
points = l * rs.rand(2, n_pts)
mask[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1
mask = ndimage.gaussian_filter(mask, sigma=l / n_pts)
res = np.logical_and(mask > mask.mean(), mask_outer)
return res - ndimage.binary_erosion(res)
# Generate synthetic images, and projections
l = 128
proj_operator = build_projection_operator(l, l / 7.)
data = generate_synthetic_data()
proj = proj_operator * data.ravel()[:, np.newaxis]
proj += 0.15 * np.random.randn(*proj.shape)
# Reconstruction with L2 (Ridge) penalization
rgr_ridge = Ridge(alpha=0.2)
rgr_ridge.fit(proj_operator, proj.ravel())
rec_l2 = rgr_ridge.coef_.reshape(l, l)
# Reconstruction with L1 (Lasso) penalization
# the best value of alpha was determined using cross validation
# with LassoCV
rgr_lasso = Lasso(alpha=0.001)
rgr_lasso.fit(proj_operator, proj.ravel())
rec_l1 = rgr_lasso.coef_.reshape(l, l)
plt.figure(figsize=(8, 3.3))
plt.subplot(131)
plt.imshow(data, cmap=plt.cm.gray, interpolation='nearest')
plt.axis('off')
plt.title('original image')
plt.subplot(132)
plt.imshow(rec_l2, cmap=plt.cm.gray, interpolation='nearest')
plt.title('L2 penalization')
plt.axis('off')
plt.subplot(133)
plt.imshow(rec_l1, cmap=plt.cm.gray, interpolation='nearest')
plt.title('L1 penalization')
plt.axis('off')
plt.subplots_adjust(hspace=0.01, wspace=0.01, top=1, bottom=0, left=0,
right=1)
plt.show()
La imagen que se obtiene es la siguiente:
Primero explicando el resultado lo que se tienen es una imagen que se crea y se toma como imagen original, la imagen del centro y la derecha son aproximaciones lineales a la original. Lo interesante es que las dos aproximaciones son buenas, pero la generada por Lasso es mucho mejor que la generada por Ridge.
¿Cómo hace esto el código? En general la idea de aplicar una regresión es para predecir datos y se piensa en la imagen de la recta o el plano que se aproxima a los datos que se tratan de modelar.
En esta caso también se hace una aproximación lineal, lo cual es generado por las funciones:
1.-generate_synthetic_data() 2.-build_projection_operator()
Entonces en resumen, lo primero que se hace es cargan las librerías requeridas, lo cual es normal en todos los códigos. Luego se definen funciones que hacen uso de las funciones base de numpy para procesar y construir matrices. Explotando esto, lo que se construyen las dos funciones mencionadas anteriormente.
Así la muestra de datos queda considerada dentro de la variable proj sobre la cual se aplica el método np.ravel(), con lo cual se aplican las dos regresiones penalizadas para hacer la aproximación lineal con la imagen original que se gurda en la variable data.
Lamento no explicar todo a mucho detalle, pero creo que los comentario de Emmanuelle son claros y los pocos conceptos que están ocultos en el código son claros con un poco de conocimiento en álgebra lineal.
Espero que aprecien el uso de los dos métodos de regresión lineal penalizados siendo usados en una aproximación lineal a un conjunto de datos diferente a lo que suele uno ver en los libros de texto.
Ejemplo 4.-Otro ejemplo con ciertos datos.
En el libro de Willi Richert y Luis Pedro Coelho, dedican dos capítulos a mostrar el uso de la regresión lineal como una herramienta para predecir el rating en un sistema de recomendación. Recomiendo leer los capítulos 7 y 8 para que sea claro como se hace uso de la regresión para éste tipo de sistemas, referencia [3]. Como ejemplo de como usar la regresión es bastante bueno, pero algo largo y no creo bueno compartirlo en el blog ya que son varios script para mostrar como funcionaria el sistema. Por ello recomiendo comprar el texto y revisar el código que comparten en su repositorio en Github para replicar y estudiar dicho ejemplo.
Un punto clave para los sistemas de recomendación es considerar el caso cuando se tienen una cantidad pequeña de usuario comparada con una gran cantidad de productos. Ejemplo, suponiendo que se va el supermercado, se tienen una cantidad de quizás 5 mil artículo o productos y se reciben en dicha tienda solo mil clientes. Construyendo la matriz con mil filas y 5 mil columnas, se tienen un problema del tipo Ρ»Ν.
Este tipo de problemas suelen aparecer mucho cuando uno analiza datos de los empleados de una empresa, sobre productos o cierto tipo de inventarios o matrices de datos que tienen que ver con los procesos de algún empresa.
En caso de considerar la regresión como un buen modelo aplicar a este tipo de datos, el problema es que se tiene una matriz de datos que no permitiría hacer una división de entre train/ test para el algoritmo, entonces como alternativa lo que se hace es emplear una técnica de Cross-Validation la cual permite elegir los parámetros de modelo con «mejor calidad».
La técnica es llamada k-fold cross-validation, lo que se hace es que se divide la muestra en k particiones y se elige una de esas como el conjunto de test y las k-1 como train. Se repite el proceso k veces y al final se eligen las k-medias de los coeficientes como los valores de los coeficientes del modelo. Dejo en las referencias los tutoriales de Andrew Moore, en el cual pueden ver en las presentaciones como funciona de manera general el método.
Sobre el código, entonces como ejemplo hago uso del código de Willi Richert y Luis Pedro Coelho con una ligera modificación para considerar el uso de Lasso y comparar los resultados.
#Módulos
import numpy as np
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.datasets import load_svmlight_file
from sklearn.linear_model import LinearRegression, LassoCV
from sklearn.cross_validation import KFold
#Cargar los datos
data, target = load_svmlight_file('data/E2006.train')
lr = LinearRegression()
# Scores:
#Estimación del modelo lineal
lr.fit(data, target)
#Estimación del modelo Lasso
lr2=LassoCV(cv=5).fit(data,target)
#Estimaciones o predicciones
pred = lr.predict(data)
pred2 = lr2.predict(data)
print('RMSE sobre los datos de entrenamiento, {:.2}'.format(np.sqrt(mean_squared_error(target, pred))))
print('R2 sobre los datos de entrenamiento, {:.2}'.format(r2_score(target, pred)))
print('')
pred = np.zeros_like(target)
kf = KFold(len(target), n_folds=5)
for train, test in kf:
lr.fit(data[train], target[train])
pred[test] = lr.predict(data[test])
print('RMSE sobre los datos de prueba (5-fold), {:.2}'.format(np.sqrt(mean_squared_error(target, pred))))
print('R2 sobre los datos de prueba (5-fold), {:.2}'.format(r2_score(target, pred)))
#Estimaciones para Lasso
print('RMSE en Lasso(5-fold), {:.2}'.format(np.sqrt(mean_squared_error(target, pred2))))
print('R2 en Lasso(5-fold), {:.2}'.format(r2_score(target, pred2)))
El código regresa cierta información, al cuales son los estadísticos básicos para saber como se comporta el modelo.
RMSE sobre los datos de entrenamiento, 0.0012 R2 sobre los datos de entrenamiento, 1.0 RMSE sobre los datos de prueba(5-fold), 0.59 R2 sobre los datos de prueba(5-fold), 0.12 RMSE en Lasso(5-fold), 0.37 R2 en Lasso(5-fold), 0.66
Si se revisan los primeros datos causa confusión, por que parecen que el primer modelo es «perfecto», pero eso es una mala señal sobre el modelo. Para más detalles dejo algunas referencias sobre sobre los estadísticos y su valoración.
Entonces con este último ejemplo la intención es mostrar que cuando se tienen condiciones del tipo Ρ»Ν lo adecuado es usar Cross-Validation para este tipo de muestras al momento de aplicar la regresión.
Varios errores que cometemos al aplicar una regresión lineal.
En un post de Cheng-Tau Chu listó 7 errores que pasan al aplicar algoritmos de Machine Learning. Eligiendo los errores que se presentan en la regresión lineal en general, la lista sería algo así:
- No revisar la correlación de los errores
- No tener varianza constante en los errores.
- No considerar la importancia de los outliers.
- No cuidar los problemas de la multicolinealidad o colinealidad en los datos.
- Considerar un modelo lineal cuando las interacciones de los datos son no-lineales.
Hablar de cada punto requiere dar un ejemplo de donde falla el modelo lineal y como abordar dicho problema. Recomiendo la referencia [2] para revisar algunos detalles.
Conclusión: Espero que los ejemplos den una idea general sobre como se usa la regresión lineal. Hay otras variaciones de la regresión que son LAR y Elastic Net, sobre las dos hay mucho material y sobre todo que son técnicas más nuevas y han estado en recientes cambios con nuevas investigaciones.
Referencias:
- https://mitpress.mit.edu/books/machine-learning-2
- http://statweb.stanford.edu/~tibs/ElemStatLearn/
- http://www.amazon.es/Building-Machine-Learning-Systems-Python/dp/1782161406
- http://www.springer.com/us/book/9780387310732





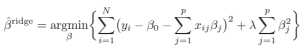



Gracias por compartir tu conocimiento, estoy tratando de afinar mi conocimiento sobre regresiones y el uso de python, y quiero replicar tu ejemplo, sin embargo no encuentro el dataset de Diabetes, sera posible que puedas compartirlo?.
Gracias!!!
Hola, perdón por no haber contestado antes. Busco los datos y te los comparto, impartí un curso junto con una buena amiga hace un par de meses, te paso el link del repositorio. Contiene un ejemplo de regresión: https://github.com/dlegor/Machine_Learning_con_Python_2017